Taking Stock
These pages have been purposely left confused
as to what it is they are aiming at,
and in something of a superposition of
assuming that we are trying to find how to build a machine
that can exhibit consciousness, or beliefs, or emotions, or semantics and meaning, or contextualisation,
passing through notions of divergence, time-reversal, story-writing, communication space,
and even the quest to find what is the aim of life.
This has been done just to experiment and play with those ideas,
and to see what might crystalise out of the discussion.
We need to be aware of
the potential pitfalls of the assumptions of the previous chapters.
The possibility of all this being used as a tool of speculation.
The ultimate goal of these chapters
has been to predict the properties of the next revolutionary machine-class,
and perhaps also to shed light on how we fit into the scheme of things.
Pitfalls of the assumptions
Many assumptions have been implicitly made in these pages:
- There is another industrial revolution, and accompanying invention of a new machine-class, yet to come
- There is an identifiable sequence to these machine-classes
- The properties of later members of the sequence
can be inferred from those of earlier ones
- Artificial consciousness is the next revolution that is waiting in the wings
Is Assumption-4 correct
(that artificial consciousness as the next revolution waiting in the wings)?
This point must be addressed.
Is Assumption-3 correct
(that the properties of later members of the sequence of machine-classes
can be inferred from those of earlier ones)?
Even if it is, we will be extrapolating new members from "a thimbleful of base cases".
Plus, there is the possibility of it being a case of pareidolia (or even apophenia):
an over eager search for patterns that might only throw up Ley lines.
Furthermore, chaotic systems have periodicity but no predictability (Gle97);
new inventions, and their emergent properties, are, by definition, difficult to predict.
Is Assumption-2 correct
(that there is a sequence of machine-classes common to the industrial revolutions)?
Even if it is, there are exceptions, as these chapters observe,
to the properties shared by computers, heat-engines and wheels.
Like tin from silicon (in the periodic table),
exponentiation from multiplication,
later members of the sequence might not inherit every property.
And, like zinc from calcium,
a pattern thrown up by a first analysis
can belie a more complicated mechanism.
Is Assumption-1 correct
(that there is another industrial revolution, and accompanying invention of a new machine-class, yet to come)?
Even if it is, it has a second side:
- Assumption-1a
- there remains at least one invention after the computer
- Assumption-1b
- the invention has not been already made
Society, used to ever-faster change,
might have become blasé, desensitised,
to new revolutions when they occur,
and to have taken the new invention already for granted.
These chapters could at least, then, be instrumental
in awarding it its deserved recognition.
Many have already trodden this ground:
John Baez, and co-authors, on the generalisation of Shannon and Turing;
and, "Programming techniques for reversible comparison sorts"
by HB Axelsen and T Yokoyama.
Heavily drawing on direct quotes from emails from Adrian West,
there is Arthur Schopenhauer's "The World as Will and Representation"
Schopenhauer viewed music
as an alternate and completely separate path to perceiving the underlying reality
that we only have indirect access to with perception.
Kant/Schopenhauer's limitation principle
(limitations of perception and inevitable distortions of any system of thinking or knowing)
that we can even ultimately in-principle know is vastly smaller it is than we think it is,
compared to what there is and can possibly be;
and Eastern philosophies
where the issues centre on relations between "reality", "perception",
and "the interconnectedness (boundaryless-ness) of phenomena".
On the difference between high intelligence and genius,
Schopenhauer also said, "Talent hits a target no one else can hit;
genius hits a target no one else can see."
Indeed, semantics-handling, theorem-proving beliefs machines already do exist
for working through the 'what-ifs' of initial axiom beliefs,
searching for implications and inconsistencies.
To generate new theories,
by dropping or inverting Euclid's fifth axiom (Bod91, Hof80),
the expert system might be the new MC
waiting for a new von Neumann / Watt to make it many times more efficient and practical
by one simple structural change.
There is plenty of scope for scepticism, even so.
But the aim of these chapters is just to be an interesting exercise,
to see what it might turn up.
Any interesting new ideas would then be worth following up
by more rigorous investigation.
Useful as a tool of speculation
One of the problems with understanding quantum physics
is that it lies outside the intuitive view in the context
of which our primate brains have evolved to work.
However, that is hopefully just a matter of time,
and noting that we do not yet have an intuitive view.
The principle of least action for mechanics was in large part
born out of the principle of least time for optics,
and Hamilton was inspired by the notion of there being a mechanical refractive index
that apples falling from trees experience.
As Lanczos noted,
"the 'particle' which represents that system
does not move in the ordinary three-dimensional space
but in an n-dimensional Reimannian manifold" (p140,
Lanczos (1949)).
It seems to have parallels with the notion of our living out our 3D+1 lives
on the 2D+1 surface of some sort of holographic universe.
The central role of the principle of least action
raises the possibility that the configuration point in the configuration space of Lagrange,
or the 'surface of common action' or phase fluid of Hamilton,
might be possible candidates for objective reality:
a group of particles,
suddenly finding itself disconnected from the apple tree that had previously been supporting it,
is guided through the varying mechanical refractive index landscape on Hamilton's phase space).
Principles of limitation
A matter handler (such as a chemical reaction vessel)
is limited by Heisenberg's Uncertainty Principle.
Neither the uncertainty of the momentum nor that of the distance can be zero.
By implication, we can also predict that
neither the momentum nor the distance can be zero, either.
Similarly, an energy handler (such as a heat engine) is limited by Heisenberg's Uncertainty Principle.
Neither the uncertainty of the amount of energy nor that of the amount of time can be zero.
By implication,
neither the amount of energy nor the amount of time can be zero, either.
This then implies the spontaneous presence of energy in the quantum vacuum
(albeit 120 orders of magnitude out, in its prediction),
as a result of Heisenberg's Uncertainty Principle, and hence of the second law of thermodynamics.
An entropy handler, too, is limited by Heisenberg's Uncertainty Principle.
Neither the uncertainty of the entropy, nor that of the temperature,
nor that of the amount of time can be zero.
By implication,
neither the entropy, nor the temperature, nor the amount of time can be zero, either.
This then implies the third law of thermodynamics
as a result of Heisenberg's Uncertainty Principle, and hence of the second law of thermodynamics.
An information handler (such as a computer) is limited by a generalisation of Turing's Halting Problem.
Neither the uncertainty of computability nor that of the execution time can be zero.
By implication,
neither the computability nor the execution time can be zero, either.
Turing machines are limited more by the uncertainity on the execution time,
while evolutionary systems
and perhaps quantum computers are able to find their way
past the Turing Halting Problem by sacraficing determinism about the computability.
A deductive logic handler is limited by Gödel's Incompleteness Theorem.
Neither the uncertainty of completeness nor that of the consistency,
nor that of the scope can be zero.
By implication,
neither the completeness, nor the consistency nor the scope can be zero, either.
It has been suggested that the long-sought theory of everything
might simply come from suitably adapting the laws of thermodynamics (NS, 13-Oct-2012, p32).
Indeed, the laws of thermodynamics are more like meta laws,
talking about how to construct other physical laws,
rather than about physical systems (NS, 17-Apr-2021, p34).
A possible process for generating a Theory of Everything,
or at least of unifying the various disciplines, one after another,
might involve the following steps:
- Find a law that states a fundamental limit in the given subject
- Show how, if it did not hold, the system could be used to build a perpetual motion machine.
Heisenberg’s Uncertainty Principle, coupled with Noether, also suggests another guideline:
- Find how to frame the limitation law as a symmetry
- Fit it into a suitable set of Lagrangian equations
- Infer the corresponding conservation law.
It can be shown that Heisenberg’s Uncertainty Principle
can be reframed in information theory terms (NS, 23-Jun-2012, p8),
with the momentum of the particle as one message stream, and its position as another,
and then questions can be asked about decoding the two message streams
(Maxwell's demon is presumably connected to this).
It shows that if Heisenberg’s Uncertainty Principle were relaxed,
then the second law of thermodynamics would be violated,
and hence that Heisenberg’s Uncertainty Principle follows from the second law of thermodynamics.
Consequently, if you did manage to find out an electron's position as well as its momentum,
you would have so much information
that you would be able to make a perpetual motion machine from it.
Relativity
Since Heisenberg's Uncertainty Principle has been demonstrated
to result from the second law of thermodynamics,
doing something similar for general relativity would then mean
that a common link would have been found between it and quantum mechanics.
Travelling faster than the speed of light would be tantamount to travel backwards in time.
Special relativity follows from the Principle of Relativity
(constant motion of the system cannot be determined by observations completely inside the system),
and the Relativity of Simultaneity (simultaneous events in one context are not simultaneous in another).
General relativity follows from generalising the Principle of Relativity still further
(momentum mass and gravitational mass are indistinguishable, and exactly equal;
therefore, even though acceleration can be felt from within the system,
since it does not constitute constant motion,
it cannot be distinguished from a gravitational field,
just by observations completely inside the system).
For a neutrino, mass and flavour form a conjugate pair,
so we know that neither of these can be zero;
but this is confirmed, too, by special relativity,
since neutrinos are able to do things mid-journey, such as to change flavour.
At the other extreme, if we were to imagine there being particles with zero rest mass
that travel in a vacuum slower than the speed of light,
we would find that their energy would be zero,
and so they could have no further consequences, would be undetectable, and hence would not even exist.
The conclusion is that
particles with rest mass must travel at below the vacuum speed of light, while
particles with no rest mass must travel at exactly the vacuum speed of light.
Slower-than-light, light-speed,
and faster-than-light are Lorentz-invarient properties that must hold for all observers.
Of the four axes in space-time,
we tend to think of time as being the odd one out,
in that we are not free to move backwards as well as forwards;
but maybe it is time that is the normal case,
and the three spatial axes are the odd ones out.
This might imply that we can only communicate in a direction that is infinite,
and not bounded by a singularity.
Not having the Lorentz term in our primate brain"s natural heuristics
leads to a failure to treat velocity as non-addititive,
and masses unable to be accelerated up to the speed of light.
Another is the orbit of electrons around the atomic nucleus;
at the moment of capture (recombination) the electron could be intuitively thought of
(semiclassically, by our heuristics-based primate minds)
as snapping into being a stationary, standing wave,
diffusely spread out statically round the nucleus of the atom.
Conjugate pairs of parameters
The two component terms of the the Turing halting problem ought to be conjugate,
with one based on the other's integral.
This also implies that the product of the two terms should have the units of action,
probably involving a scaling by ln(2) (to convert bits to nats)
and by Boltzmann's constant to convert to SI units.
This would probably require an adjustment to allow for the digital world
to be modelled as if it had analogue behaviour.
One intriguing idea is to take Floyd-Hoare's inductive assertions, or similar techniques,
perhaps smoothed out over notional partial cycles,
and to see if it can be used to cancel out internal movements of data during a cycle of an algorithm,
in the same way that Carnot did for internal motions within a mechanical engine,
and to see how this might tie in with Bennett's reversible computing (Sci.Amer, Jul-1985, p38).
Having such a conjugate pair,
this would then imply that neither of the terms can be reduced to zero,
since that would be a value with zero uncertainty;
but then we knew that already for execution time,
and for the computation information temperature
it probably simply implies a generalisation of the third law of thermodynamics.
After that, we might expect the symmetry in one term
to imply a conservation law in the other (Neuenschwander 2011).
We would have to work out how this maps on to
the notions of execution time and computation information temperature.
Then, the way that one term is derived from the Fourier transform of the other
would imply a wave interpretation of the system;
we would have to work out what would be the implications of this.
|
Noether's theorem confirms that
the two parameters in Heisenberg's uncertainty principle are connected
(the conservation law of one follows as a consequence of the symmetry exhibited by the other)
and hence that the two parameters are just two sides of the same coin,
so are described by one shared set of information, not two.
Heisenberg, Noether, Fourier and Bell all point in the same direction,
that it is not just that we do not have access to all the information,
but that the information simply does not exist in the first place
(for example of a particle's position and of its momentum)
and that our observations can only ever be probabilistic (NS, 14-Mar-2015, p28).
A particle cannot be pin-pointed, at sub-atomic scales,
in phase-space (x,y,z,ẋ,ẏ,ż)
because the particle has only a blurred location in that space,
giving us limited ability for dead-reckoning
to extrapolate or to interpolate a particle's position.
This happens whenever we try to find partial information about an entangled system,
and perhaps indicates
that quantum weirdness simply emerges from more logical central principles (NS, 11-Apr-2015, p34).
|
Power is the rate of change of energy in time,
and, by the same token, force is the rate of change of energy in distance;
but force is also rate of change of momentum in time.
The left-hand lattice has been arranged so that by starting at any given node,
travelling southwest involves taking the d/dt, travelling southeast involves taking the d/dx
(and vice versa with integrals for travelling northeast and northwest).
Travelling horizontally, right to left, involves multiplying by dx/dt.
| | | | | | | | |
| | Z | |
| | / \ | |
| | L | mx | |
| | / \ | / \ | |
| | E | p | m | |
| | / \ | / \ | / \ | |
| P | F | m/t | m/x |
|
|
| | | | | | | | |
| | f | |
| | / \ | |
| | v | θ | |
| | / \ | / \ | |
| | xv | x | t | |
| | / \ | / \ | / \ | |
| V/t | A | xt | t2 |
|
The right-hand lattice is the mirror image of the left-hand one.
P=power, E=energy, F=force, p=momentum, m=mass, L=angular momentum, θ=angle,
mx=mass*distance (the conjugate pair for velocity),
A=area (the pair of rate of change of mass),
and Z=∫L.dt=∫m.x.dx (the pair of frequency).
|
For something to be persistent, its properties must be sustainably conserved,
and, by Noether's theorem, to manifest corresponding symmetries.
The transfer of energy and the transfer of momentum go hand-in-hand;
you cannot have one without the other.
A packet of conserved energy and momentum,
which does indeed to seem to pass through a Newton's cradle,
must manifest as the energy and momentum of something,
but are otherwise indifferent as to precisely which ball(s) are used to carry that packet
(provided that they do obey those laws of conservation).
The quantum Cheshire-cat effect
demonstrates how a particle can be made to follow one path,
while its conserved properties (such as spin)
can be made to follow a different one (NS, 26-Jul-2014, p32).
Similarly for a wave, where the one that is received at the receiver
is not the one that was transmitted,
as witnessed by the dance of the phase velocity outstrips the group velocity.
Subatomic particles are indistinguishable from one another,
with the ones emerging from an elastic collision in a Feynman diagram
are not the ones that had entered, but just carriers of the conserved information.
Similarly, in the quantum mirage experiment,
a cobalt atom at one focus of an elliptical ring of 36 other cobalt atoms,
the properties of a virtual cobalt atom appears at the other focus (NS, 08-Jul-2000).
Duality
The duality between the realm of voltage sources, impedances and electric fields,
versus that of current sources, admittances and magnetic fields, suggests, perhaps,
that the roles of symmetry and conserved quantities can be likewise interchanged,
leading to a duality between symmetry and the conserved quantity.
The overall conserved quantity appears, when viewed externally,
to exhibit a symmetry,
even though internally it contains a dynamic system.
Kirchhoff's current law is a statement about conserved quantities (electrical charge);
Kirchhoff's voltage law is a statement about symmetry (such as the choise of reference voltage).
Both involve sigma summations over the various arcs of an electrical circuit,
originally containing just resistors and voltage sources,
but easily generalisable to containing inductors and capacitors
(along with the notion of a displacement current
continuing on through the gap between the capacitor plates).
When generalised further, to continuous integration in space, they yield two of the Maxwell's equations.
The other two of Maxwell's equations are generated for repeating the process for magnetic circuits
(and, as a very last step, setting the number of magnetic monopoles to zero).
|
Kirchhoff's current law takes the circuit star-connected nodes, one at a time.
Kirchhoff's voltage law takes the circuit one delta-connected loop at a time.
But, star and delta connections can be interchanged,
as shown in Rosen's theorem.
Perhaps the voltage law can be re-expressed as a star-connected conservation law,
and the current law can be re-expressed as a symmetry of nodes round a loop.
Such an extreme view would allow us to depict time differences around a system of components, at equilibrium,
and energy conservation via a summation to zero at the nodes;
and then, alternatively, energy drops around a circuit of components (energy rises through active components),
and time flow (whatever that means) summing to zero at the nodes (whatever that means).
The impedances in such a circuit would have the dimensions of power.
|
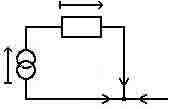
|
If we then repeat the exercise for momentum and space,
the impedances in the circuit would have the dimensions of mass/time
(which is also the dimensions for water current).
However, we can return to the electrical version of the circuit,
and note that Kirchhoff's current law is talking about the conservation of charge-per-unit-time.
The energy-time circuit should therefore be redrawn as a power-time circuit,
or as an energy-scalar circuit (the scalar being dw/dt, the rate of flow of time per unit time),
with the impedances having the dimensions of energy.
The momentum-space circuit would then be redrawn as a force-space circuit,
with the impedances having the dimensions of mass/time-squared,
or better as a momentum-velocity circuit,
with the impedances having the dimensions of mass.
The transform converts activities (on the arcs) into events (at the nodes) and vice versa.
Meanwhile, Fourier transforms convert features in the time domain into features in the frequency domain.
If information is a conserved quantity in quantum mechanics and relativity,
we need to establish what is the corresponding symmetry,
perhaps a generalisation of Floyd-Hoare loop-invariant properties (inductive assertions).
Since E=S.T, it follows that dE/dt=T.dS/dt+S.dT/dt.
Heating a beaker of water first prefers the former term,
maximising the increase in entropy while keeping the temperature constrant
(not least at the point of phase-change),
and only then resorts to increasing the temperature while keeping the entropy maximally constant.
The dS/dt term has hints of dw/dt about it,
suggesting that, at thermodynamic equilibrium,
zero change in entropy would appear internally as no passage of time.
Concluding remarks
This section has considered:
principles of limitation and
relativity and
conjugate pairs of parameters and
duality.
Comparative control experiments, and a generalised parallax effect.
Kirchhoff's voltage (symmetry) and current (conservation) laws:
latency and throughput of pipelines, and the devices of Shannon, Carnot and Turing.
Probabilities expressed as half-life.
The selective (symmetry-breaking) properties of
resonnance, filters, and generalised standing-waves.
Are we able to predict the nature of the next machine-class?
Each cultural revolution and its enabling technology (wheel, steam engine, computer)
can be viewed as just another layer of convection current
driven on by the second law of thermodynamics.
From a bottom-up, engineering perspective,
can new insights lead us to the design of revolutionary new machines
to help us feed the ever growing population?
These chapters have explored a number of different models for identifying such
a new type of machine.
Though these pages have provided a hotch-potch check-list against which to test ideas,
they have failed, so far, to propose a new intuition, Faraday-like,
to help us design any new machine.
These pages have been in something of a superposition of
assuming that we are trying to find how to build a machine
that can exhibit consciousness, or beliefs, or emotions, or semantics and meaning, or contextualisation,
passing through notions of divergence, time-reversal, story-writing, communication space,
and even the quest to find what is the aim of life.
They have even hovered in a superposition of the stances
of materialisn, Idealism,
panpsychism, existentialism,
eternalism, and presentism,
to name just a few.
But maybe that is the point.
In the second chapter, the suggestion was made,
in the section on building machines upon machines,
that the next machine-class might be constructed from computing machine parts,
with each computer constrained from executing its program directly from beginning to end.
And this is what each paragraph of these pages has tended to do:
to follow an argument just so far, before restarting in the next paragraph on a different idea,
not necessarily compatible with the previous one.
The generalised parallax effect then allows new paragraphs then to remark on the differences between
those previous paragraphs, and to infer possible implications.
Chapter two does indeed also propose the process of document-writing
as a strong contender as a model for how the next MC might be expected to work.
One intriguing possibility is that this oscillation between paragraphs
could be a route to bringing software engineering into the same fold as the other branches of engineering.
Clearly, it does qualify as being considered a branch of engineering
since the word engineering indicates the arranging for something to be constructed.
However, the other branches of engineering all allow for simple harmonic motion,
described by a differential equation of the form "V=L.d2q/dt2+R.dq/dt+(1/C).q".
How do we fit into the scheme of things?
As noted above, these pages have been vague as to whether
the aim is to seek out a lucrative revolutionary engineering idea;
or one that promises to make the world a better place;
or whether it is to seek a idea that would go on to help mankind better understand how the universe works;
or even to help us to understand what the underlying reason is for our existence.
The way that the human brain works is to package things up as modules,
and then to handled the module as if it were a fundamental object;
that is, we tag those modules with a name,
and then handle that concept symbolically using that tag from then on.
The human brain is capable of coming up with tags for all sorts of concepts,
such as unicorns, griffins, luminiferous aether, phlogiston.
This neither proves that those concepts are real, nor does it prove directly that they are imaginary.
That requires further observation and reasoning,
which is why we give them names so that we can handle them with our symbol-manipulating minds.
So we come, inevitably, to the question of whether God exists
(or any of the other specific names given by the various religions and their sub-divisions round the world).
Well the tag stands for something.
But is the concept is grounded in reality, or just in our thoughts?
Some would answer, "grounded in reality," and others "just in our thoughts".
Doubtless, we are no closer to a definitive answer
than the finest thinkers have managed over the past millennia.
Science needs to keep visiting what are presently metaphysical questions,
to see if new progress can be made, in the light of new knowledge (NS, 03-Sep-2016, p28),
including those of consciousness (p31),
why there is something rather than nothing (p32),
free-will (p35),
what reality is made of (p36),
whether time is just an illusion (p37),
and whether God exists (p39).
Somewhat superficially, and through speculative pattern-matching,
we could note the underlying hope as being a striving to follow our steadfast guide,
in a universe that started well away from equilibrium,
that provides the regular flow of low-entropy input,
and thereby allows the building up of structures
that need to avoid the pitfalls of singularly deep minima,
and getting caught up be local maxima,
and the need to tolerate a certain level of trespassing on each other's extended phenotypes,
as their own,
and to keep to the guide with all the traits that we can amplify
with that extended phenotype.
- The next machine-class as a sequence
- Two models of the next machine-class built on computing technology
- Inevitable emergence of structure
- Symbiotic subservience to another organism
- Dennett-like self-writing documents
Back to the initial assertions of these pages.
|

