 |
English | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Home page | Services | Past achievements | Contact | Site map |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Page d'accueil | Services | Réalisations précédentes | Contact | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Français | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
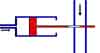
Figure 1. Enhancement Mode Pneumatic Transistor |
First, in a digital computer, a gas (electron or molecular) travels from the distant pressure generator, through the supply pipe, to power switches (enhancement or depletion mode, Figures 1 and 2) (where the pressure of the fluid in one pipe controls the flow in a wider one) and returns to "air" by the exhaust pipe. In this way, it would be conceptually possible to take the electronic circuit schematic for a simple processor and replace each of the electronic components literally by pneumatic or hydraulic ones. |

Figure 2. Depletion Mode Pneumatic Transistor |
As a second, distinct model, consider a locomotive reading its microcode up and down the Turing track, acting as the read/write scanner-head of a Universal Turing Machine. It is a full sized locomotive that can steam along the line, but with, on board, the state logic of a pneumatic version of the read/write scanner-head.
|
The railway sleepers could form the Turing tape, with mechanical flip-flops mounted across each one, of the inverted pendulum type (Figure 3). The locomotive would have valves that open and close, on brushing by the flip-flops on the current sleeper, with steam actuators to change their settings when required. Although the locomotive is capable of travelling full steam, from Paddington to Temple Meads, it spends its working life, now, edging up and down a few kilometres of its track. |

Figure 3. Inverted Pendulum Flip-Flop |
Although not making progress, by the normal measure of steam locomotive performance, it would be making computational progress on the data that the programmer had stored in the flip-flops. Likewise, the next MC modelled with a computer parts would be constrained from making forward progress in executing its program. The computer would be made to run backwards in some seemingly erratic, but in actual fact well controlled, way. A small, not normally expected, extra input would be overriding the normal progress of the computer, like the seemingly minor addition of flip-flops on the railway sleepers overriding the locomotive's normal behaviour.
Although the locomotive is constrained from travelling full steam, its peak speed is still important, and determines the computing speed of the Turing machine. Likewise, a one Mips computer would do one million parts of next MC work per second, although no longer executing consistently towards completing the given computation.
Processing as a type of communication
There are three principle functions that are common to all computers, whether imperative or declarative, that have ever been built, designed, or merely contemplated: processing, memory and communications.
|
Communication involves the transfer of information over space, and memory involves the transfer of information over time (albeit only in the forward direction). It is not surprising, therefore, that the two are similar, and are analysed in the same way in Shannon information theory: represented on a "T" diagram, with input data coming in from the left of the diagram, output data leaving from the right, and noise being injected by the medium from the third arm. It is tempting to wonder whether processing, too, can be considered in the same way, as a type of communication, though also noting that processing is the odd one out, since the other two are already united in their reference to the four dimensions of space-time. |
In by-gone days, I wrote my files to floppy disk at night, communicating them to the future, to read back the next day (perhaps on another computer). When I read my files from floppy disk the next day, to write back that night (having edited or otherwise modified them) was I communicating in some way? I would say “I am editing” or “I am compiling” or “I am processing”.
|
"To edit" is to merge two streams of data: the old version of the syntactic information from the disk, and the incremental semantic changes within my head. “To compile” is to merge the syntactic source code information (already on the disk) with semantic rewrite rules embodied by the compiler. "To process" is to merge the syntactic input file with semantic rewrite rules embodied by the instruction set (or perhaps with yet another level of rewrite rules embodied in the microcode). |

|
Processing is necessary for presenting information (such as tables, graphs, lists, and diagrams); and for syntactic-compression, too, for transmission or storage. The informed user sends information to the uninformed user in a different mind-set. One user has raw data, and has to work out the results (maybe in his head); the other is given the results, ready and all worked out. Processing is necessary to establish relevance. You want to learn about the Cretacianeous period? Here is a mountain of limestone layers. You want to learn how to use your HP Vectra PC? Here are the circuit diagrams and object code. You want to learn about parquet flooring? Here is an un-indexed pile of back-issues of DIY magazines. You want to learn about the Norman Conquest? Here are the current positions and velocities of all the particles in the universe. This is related to the question of whether chaotic outcomes, such as the value of the next pixel in a Mandelbrot set, is pre-computable like the outcome of a coin being tossed.
|
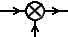
The communication theorists' coat of arms, taking on the shape of a T, can be treated as a block in a circuit diagram, with a stream of 1s and 0s coming from the input, being merged in an exclusive-or gate with a stream of 1s and 0s coming from the noise input. |
[Input]--->---[channel]--->---[Output]
|
^
|
[Noise]
|
Both Shannon and Turing abstracted away from the details of the implementation. A channel carries information, regardless of what that information might be (and there are no violins inside the jukebox); a computation proceeds through the steps of the algorithm, regardless of the hardware that is being used. Shannon devised a universal information carrier, and Turing devised a universal computable-numbers machine. So what we seek now is a universal consciousness machine, looking for stable patterns on which it can further build, by relaxing (increasing) the annealing temperature ('willing' the system up to the next stable platform, capable of being packaged up mentally as an autonomous black-box module, on which to build further.

|
With Shannon information, the input can be represented just as a 2x1 matrix of probabilities of a 1 occurring, or a 0, and the noise input by a 2x2 matrix of the probabilities of a 1 being corrupted to a 0, or vice versa, or to go through unchanged. For this, the operation represented by the block at the node of the T is that of matrix multiplication. |
|
The Shannon "T" diagram can be extended to "TTT", where the middle "T" still represents the point at which noise is being injected by the medium, but the first "T" injects a transformation (G) on the input data, and the last "T" injects the inverse transformation (H) to reconstitute the original data (Moser and Chen, 2012). |



|
Traditionally, over a low-noise medium (still on the second "T") Gl can implement data compression, and Hl its inverse decompression; while over a high-noise medium, Gh can add a redundant coding, and Hh its inverse decoding. So, perhaps processing can be modelled using a similar diagram, via the G or H function. Since the action of a computer is to reduce information content, somewhat akin to Michelangelo chiselling out the redundant information to reveal the inner sculpture, we could either model the microcode of the processor as Gl in the low-noise medium, or Hh in the high-noise medium. The former would have Hl as some sort of anti-processing function, able (hypothetically) to beat the Turing Halting Problem. Alternatively, the latter model would have Gh as some sort of obfuscating process. A human example of this might be the universe obeying very simple laws, like those of the principle of least action (Coopersmith 2017) but presenting very complicated emergent behaviour to us on the first "T", with Tycho Brahe's telescope at the second "T", and Kepler's tomographic processing of the data back down to simple laws at the last "T". (Similarly for Faraday and Maxwell.)
Reversibilty
One question that this then poses is whether it is necessary to consider the inverse transformation of Turing processing, even if it is not used in general practice. This might require the CPU to be implemented as a reversible computer, using Fredkin gates rather than information-destroying NAND and NOR. However, the Turing locomotive executing the algorithm on the Turing track, made no attempt to be Carnot reversible. Indeed, with the electronic computer, electrical-engineering energy and information are dissipated liberally. In a similar way, the contents of the living cell are maintained in a low-entropy state, at the cost of having to take in low-entropy nutrients from outside, and to expel high-entropy waste products back out again.
The Carnot cycle involves energy transfer, and takes infinitely long to complete as the temperature differential approaches zero, and involves gain in entropy otherwise. Similarly, computing involves information transfer, as described by Shannon, even if Fredkin gates are used, to sort the wanted information from the discarded information. Again, entropy must increase as the stuff that encodes that information is shifted from over here to over there (though perhaps spring-loaded, so that that energy can be recouperated in the reverse operation). Getting a project implemented must involve activity, as remarked by Hodges 1992, p422 as a point that Turing personally failed to take into account.
The locomotive could be transporting information, in its train of carriages, from Paddington to Temple Meads; working as a UTM though, that information never arrives there, though it is still delivered either to the output or to the waste-area. If the information in the carriages is used en route, it becomes part of the state machine. Analogous to Kirchhoff's current law, if more information is flowing in to a point than is flowing out, the surplus must either be going in to storage or else leaking out as dissipation. (If more information is flowing out of a point than is flowing in, the surplus must either be coming out of storage (and erased from there) or else leaking in from the outside, either way involving the in-flow of energy.)
Whether it be in the imperative language model, as might be appropriate for Bennett's Brownian-motion computer mechanism (Sci.Amer, Jul-1985, p38) or in a declarative language model, computation is the monotonic process of reducing the algorithmic entropy, K, and hence the degrees of freedom in the semantic context, as it progresses towards the ground state of normal form (halting-problem permitting). Reversing the process of lambda calculus reduction, pseudo-semantics and pseudo-context are inevitably added to the input string; the inverse of beta or alpha reduction (beta or alpha expansion) might come up with the number of sides of a hexagon being "factorial(3)" or perhaps "the number of balls in a cricket over". With genetic mutation, in particular, and bifurcation, in general, the vast majority of points where it occurs will appear random, and meaningless. Where they do happen to hit on a new sequence that has meaning, that new meaning will have arisen at random, and be inserted into the existing sequence. For instance, returning to the example of the number of sides of a hexagon, randomly equating it to the number of angles in two triangles, might (or might not) serendipitously discover a new property in mathematics.
Topological, passive and active
The table, below, started out just as the column headed "Memory" and noted that there are three types of implementation of memory, and that they can be categorised as: communications-based (delay line), pure memory based (decay law), and processing based (regenerative gating). For the first two, unintentional losses, and divergent collisions with molecules of the environment, lead to an exponential decay-law and corresponding time-constant, or half-life); while, for the last case, the unintentional losses are compensated for, via an amplifier, and energy input exponentially growing until saturation (clipped at a physical limit).
|
The wiring, Z=NOR(X,Y), results in the loss of information (if Z is a 1, the values of X and Y are known precisely, but if Z is a 0, there is only a 1-in-3 chance of guessing the correct values of X and Y), so, the "Qbar=NOR(Q,S); Q=NOR(Qbar,R)" SR flip-flop circuit uses this to implement a standard memory cell. It also shows that the laying down of memory, the direction of the processing, and the information destruction of Landauer's principle, are all consistent. |
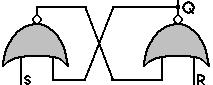
|
Delay-line memory is an example of how communication in space can be turned into memory simply by looping the communication channel back to the transmitter, and demonstrates the intimate relationship between the way we measure time, and the entropy increase that is involved in memory storage. Similarly, communication in space can be implemented by decay-law memory, simply by transporting the object (for example, ink marks on a sheet of paper can be physically transferred in the postal system, and USB memory sticks can be carried to a new destination).
Speech was an invention between the lever and the wheel; for communicating information (communicating it in space). Writing (and later printing): an invention between the wheel and heat-engine was for communicating information, and of holding it in memory, too (communicating it in time, albeit only forwards). The telephone (and later email) was an invention between the heat-engine and computer; for communicating information, and memory and processing (with deductive logic in the telephone exchange). The Semantics System will be an invention between the computer and the next MC; for communicating, memorising, processing information, and something else: contextualisation, perhaps. The Empathy System will be an invention between the next MC and the MC after that.
| Communications | Memory | Processing | Contextualisation | Empathy | |
|---|---|---|---|---|---|
| Speech and I/O | passive (spatial decay-law) | topological (delay line) | |||
| Writing and storage | active (tangible) | passive (temporal decay-law) | topological (mapped on the page) | ||
| Processing and CPU | active (regenerative) | passive (conventional computation) | topological (mapped on the page) | ||
| Semantics and Next MC | active (Platonic space) | passive | topological | ||
| Empathy and MC after that | active | passive |
Human speech is passive communication: the message travelling from one person's mouth to the other's ear (Table above). Human speech is topological memory: folk history passed down the generations by delay-line word-of-mouth. Human writing is active communication: written communications are more concrete than spoken ones; and written contracts more than oral ones. Human writing is passive memory: ink on paper has a time constant. Human writing (like this text) is topological processing: the successive states of a computation mapped out across the page (Table below). Human processing is active memory: regeneratively repeating something over and over while it is still being needed. Human processing is passive processing: by the same token as the naming of passive communication and passive memory. Human processing is topological contextualisation: whatever the next MC does. The human equivalent of the next MC is active processing: mathematicians discover truths in Platonic space, perhaps. The human equivalent of the next MC is passive contextualisation: whatever the next MC does. The human equivalent of the next MC is topological empathy: whatever the MC after that does.
In speech, it is the human mind that provides the memory; passing down a story by word-of-mouth. In writing, it is the human mind that provides the processing. In computing, it is the human mind that provides the semantics, appreciated by the programmer, not the computer. The value '6', in 'CELL', is ungrounded without the external context: is it six dollars, six balls in a cricket over, six sides for a polygon, sixth time round the loop, a RTT instruction, or something else?
| a | b | r | |
|---|---|---|---|
| 33932 | 68034 | ||
| 1: r := a mod b | 33932, 170, 102, 68, 34, 0 | ||
| 2: a := b | 68034, 33932, 170, 102, 68, 34 | ||
| 3: b := r | 33932, 170, 102, 68, 34, 0 | ||
| 4: IF b > 0 THEN GOTO 1 |
This rolls out in time as depicted in the following table. The column on the left contains the contents of the program counter (which might or might not be memory-mapped, cycling six times over the labels for L1, L2, L3 and L4; each cell can either show no change in its value, or a single new value written in; and the four instructions are listed horizontally along with a, b and r (assuming a stored-program architecture) just as an array of variables would be depicted, indexed by the program counter, but with values that are never changed (since there is no self-modifying code).
| PC | a | b | r | L0 | L1 | L2 | L3 | L4 | L5 |
|---|---|---|---|---|---|---|---|---|---|
| L1 | 33932 | 68034 | NOP | r := a mod b | a := b | b := r | IF b > 0 THEN GOTO L1 | HALT | |
| L2 | 33932 | ||||||||
| L3 | 68034 | ||||||||
| L4 | 33932 | ||||||||
| L1 | |||||||||
| L2 | 170 | ||||||||
| L3 | 33932 | ||||||||
| L4 | 170 | ||||||||
| L1 | |||||||||
| L2 | 102 | ||||||||
| L3 | 170 | ||||||||
| L4 | 102 | ||||||||
| L1 | |||||||||
| L2 | 68 | ||||||||
| L3 | 102 | ||||||||
| L4 | 68 | ||||||||
| L1 | |||||||||
| L2 | 34 | ||||||||
| L3 | 68 | ||||||||
| L4 | 34 | ||||||||
| L1 | |||||||||
| L2 | 0 | ||||||||
| L3 | 34 | ||||||||
| L4 | 0 | ||||||||
| L5 |
Concluding remarks
Each of the three principle functions that are common to all computers, namely processing, memory and communications, can be characterised by measures of latency and throughput (where the throughput tends to be called the bandwidth, in the case of communications, and the latency tends be called the execution time, in the case of processing). Consequently, this section has considered processing as a type of communication, and reversibilty, and topological, passive and active. This information flow can be tied in with generalised versions of Kirchhoff's voltage (symmetry) and current (conservation)laws, and Carnot's notions of reversibility.
This starts to hint at a connection with probabilities expressed as half-life. It has not yet tied in with comparative control experiments and a generalised parallax effect. Likewise, not yet with the selective (symmetry-breaking) properties of resonnance, filters, and generalised standing-waves.
Model of the thinking mind as a self-writing story
These chapters are presently lacking a concrete sense of direction. At the next MC level on from the present ones, are we talking about semantics, meaning, contextualisation, empathy, beliefs, consciousness? The last of these is often likened to a self-authoring narrative. Perhaps simply arranging for the steam locomotive on the track to author a story. Stories acquire new information each time they are retold (Alan Turing sipping the froth of his glass of beer, Kate Bennett saying "save your breath to cool your porridge", Dawkins on the use of "virgin" as the translation, in place of "maiden".) Just as a pencil balanced on its point acquires new initial-condition, breaking-symmetry information as it starts to fall. Jane Austen dramatisations presented as nice and rosey stories (Persuasion, BBC, 1971), rather than as agreessively biting observations of human nature (Persuasion, BBC, 1995), or orchestrations of Bohemian Rhapsody as sweet gentle tunes.
Homo sapiens evolved as social animals, so our brains are wired for this sort of way of organising thoughts. At the very least, this makes social interaction a useful tool, even for such tasks as document-writing: for the author to treat the document as another entity with which to converse and interact.
Top-down versus bottom-up working
The discussion on reversibilty is pointing in the direction of modularity and identity being the preserved quantity, of the contents of the living cell, or of the data of the BubbleSort algorithm.
In computer evolutionary systems (such as GPs, GAs, and ANNs) the training data (or fitness function) is applying the top-down influence on the execution, while the annealing temperature is providing the bottom-up manipulations. In the case of natural evolutionary systems, though, there is no top-down mechanism, and it is serendipity and persistence (regions of convergence within the peaks and troughs of the landscape) that are the nearest to top-down influence (reading information from the terrain).
However, serendipity is always a fait accompli; human consciousness includes projects, and dreams of what might be engineered in the future if manipulated appropriately. This involves a mind: one that probably evolved to remember the past (such as when to sow seeds and harvest crops) for driving the behaviour again this time round; but one that can also remember (as in, "imagine") a desirable future (such as moving to new fields, or changing to new crops) again for driving the behaviour this time round. Not just a remembered present, but a remembered future, along with a drive to follow through the feeling of, "if only things were like this". An intentional stance. Mentally walking around a remembered past, for example trying to remember where one might have mislaid an object, and mentally walking around a remembered future, to imagine the consequences of a new project.
Computer algorithms, such as BubbleSort, are convergent processes, so require more effort (memory) to reverse exactly. However, maybe exact reversal is not what is required. Maybe reverse-BubbleSort merely needs to change the list back to one that is of an equal level of unsortedness as the original: dissipating the information of the original list to leave another that is just about equivalent. Similarly, an execution tree, reducing in size by evaluating the leaf nodes first, can be reversed to create a bigger execution tree that is different to the original, but executes (when run forwards again) to yield the same result. With the Brownian-motion reversible computer (Sci.Amer, Jul-1985, p38) temporarily running backwards, any instruction could be written as the previous contents of the instruction register. In many ways, this is what a story-teller does: starting from the final desired effect, and then working out how the characters might have arrived there.
Parallax-like comparison of comparing different ways of arriving at the same conclusion: double-entry book-keeping, cross-checking mathematical results, two routes diagonally across a parallelogram. Cross-checking of reports from different senses of a given event, as in Dennett's multiple drafts model. For the opposite process, science is forever looking to identify the invarient properties of systems.
The tautological property that stable structures outlive unstable ones is used in GAs, GPs, classifier systems, simulated annealing, Boltzmann machines and ANNs. With a computer evolutionary system, it is the training data that remains constant through all the annealing. The training data, or fitness function, applies the top-down control, while the repeated attempts at matching it are implementations from the bottom-up. Indeed, "1,1,2,6,24,120,720" is just as good an ASCII character name for a function as "factorial" is. In the same vein, this story has been given the top-down name of towards artificial consciousness, and its individual chapters have been given similarly guiding titles, and another of these web-pages has been given the name, Quantum gravity, time and underlying objective reality: the main aim was to let the data (the in coming index items) steer the shaping up of the overall patchwork. It is like adding grains of sand to a sand-pile, and occasionally provoking avalanches of varying magnitudes, as the pieces re-arrange themselves, also exhibited in the fractal form taken by pieces of music.
The main weakness with such a bottom-up, Monte Carlo, steering is the risk of it being aimless. To be a useful tool, the self-writing story needs to be directed. Within human organisations, the bosses and leaders attempt to steer the progress through persuasive arguments in conversation. Likewise, for a document, the author needs to step in with a top-down executive control of the story, such as by setting the title of the document, and its underlying chapter headings, akin to externally-applied training data. In the case of a self-writing thesis, the document starts off with a very stong sense of direction (the thesis title, given by the supervisor on day-1); in the case of a conference announcement, the scope is usually more open, as for example in, "What is the world like, according to quantum mechanics?".
It is tempting to suggest that the author could try imposing a specific, wishful-thinking like title, artificially. However, it would simply then be found that the document has little to say on the subject. So, the initial step has to be to start with the bottom-up process, to see what sorts of things the document might have an opinion on.
Dialogue and brainstorming
The use of dialogue to argue ideas through, as explored by Plato and Socrates, Salviati and Simplicio (via Sagredo), Archilles and the Tortoise, Elizabeth Bennett and Jane Bennett (and, indeed with any of the characters she engages with), presumably Jane Austen and Cassandra Austen (and Dennett's partial conscious systems). The author could be bouncing tentative ideas off another mind, perhaps being in two minds on the given subject. Whittling out inconsistent ideas, like cracking Suduko puzzles and Enigma codes.
Perhaps Blackmore's (2017) book on Consciousness could have ended at the page on memes (p129). Hadrian's wall, for example, is a meme: the vision of one man to construct it, followed the philosophical change it created in packaging up one's thinking on the Roman Empire, and the survival advantage generated by the structure (whether physically from its defencive structure, or psychologically for those tasked with defending the Roman Empire). Similarly with the defenses contracted by William I and Henry VIII. Similarly, then, the men of vision who push for the construction of other infrastructure, such as the cannal system, the railways, the internet. Enabling technology that does not directly put food on people's tables, but increases the productivity of those who do. Similarly for the invention of writing, around the time of the ancient Egyptians, as an enabling technology for the Egyptian administrative and beliefs systems. The consciousness has gone out into its extended phenotype.
Bottom-up: Rewards, fitness, persistence/inherited-attributes. Not random emergence from an infinite typing-pool of monkeys, but juxtaposition of ideas, perhaps from brainstorming. Back-tracking is still convergent behaviour, since the back-tracked path is remembered as having been processed, and is never taken again.
Top-down: Does information drive the machine forward? Cycles within cycles, PMC (delay lines and canals). Dissipation of meaning, half-life), principle of limitation (like emergent behaviour and TD2). Human story-telling is topological processing (contextualisation, or whatever the next MC does).
What is the role of information in a project? Walking round a carboot-sale gives one clue. Each object looked at, at random, causes the mind to consider, "What if I bought this?" A quick reflection simulates the hypothetical future, and returns a one-bit decision whether to buy or not to buy. This again suggests serendipity as being required as the initial trigger, followed by a more directed building on the initial idea.
Ontological versus epistemic
Ontological models are those that reflect on the underlying mechanisms of the universe, while epistemic models are those that are merely mental tools to help us when calculating the overall behaviour. Normally, this distinction is made in the context of the various interpretations of quantum mechanics. In particular, the concept of wave-function collapse seems to be merely a human tool to analyse the behaviour. It is in the human mind that two particles are independently travelling through space, or undergoing the repercussions of a recent collision. The human mind flips from considering their wave-functions indepentently, or evolving as one entity; it is in the human mind that the probes of the experimental apparatus can somehow be parachuted in, and then abstracted back out of consideration. Wave-particle duality stems from non-local distribution of the wave function combined with the localised properties of interacting particles.
Decoherence is a type of dissipation, as by the same token, the concept of entropy, too, is in the mind, and hence too the thermodynamics arrow of time. So, too, the meaning of probability functions, entanglement, and wave-collapse. Also, seeing forever-increasing logarithmical scales as being cyclic, such as the octaves of the musical scale, and even in linear contexts such as the International Dateline, or the cycle of life. The modulus addition of fixed-length integers, ignoring the carry-bit generated in the process; indeed, the meaning of integers, in general, on computers, as noted by Turing (Hodges 1992, p327) for the meaning of pulses within the circuitry of ACE. Similarly, in human culture, dictionaries define words in terms of other words, and encyclopediae are as their name suggests. These circular definitions need, at some point, to be grounded, as a means of resolving the hard problem.
The human brain works with heuristics, analogies, and simplified models. The blending of Newtonian mechanics into special relativity via the Lorentz term, 1/√(1-v2/c2) is a fine example. The superbly heuristics-based brain that we inherit from our Stoneage ancestors finds it hard to throw off the conviction that velocities are additive (when throwing a projectile from a moving platform, for example, or colliding two moving platforms). In effect, this amounts to finding it hard to accept that the speed of light is just very large, as opposed to infinite.
it is an artifact of the way the human brain works, by economising on the thought required, by packaging chunks up as modules, giving them a name, and hence forth handling them symbolically. The human mind is finite, and somewhat limited. Indeed, we can only handle complexity if we can modularise it, and handle it at distinct, autonomous levels, via symbols. Moreover, the universe does not care about macro objects; these are all just constructions in the minds of the observer (usually human, in the examples that we consider) whose brain works on heuristics, and finds advantage in packaging things up as modules, so that it is easier to handle with far fewer parameters.
Black-box modular identity
Even something as simple as a chair is not a well-defined object: even a convenient rock or fallen tree trunk will qualify on a picnic. Even an intentionally made chair is not a well-delineated object: it is continuously exchanging its outmost layer of surface atoms and molecules with the atmosphere, the floor, and the bottom of any person who happens to sit on it. Naming objects, tagging them, is mentally convenient, allowing the heuristic brain to cut down the amount of computation required (handling the chair, mentally, as a single particle, rather than tracking all 1026, or more, of its constituents invidually). This all highlights the part being played by the human mind's heuristic of packaging groups of components into quasi-autonomous modules with outwardly black-box behaviour, such as what constitutes a chair.
It is humans that decide that one bundle of molecules should be called a chair, and handled as a stand-alone module; it is not those molecules that decide to be treated collectively as a stand-alone module. However, a passing cat is also likely to treat a chair as an identifiable module: not for quite the same purposes as the human (more as a plateau, from which to view the environment, or else a defensible position in which to curl up and go to sleep). Similarly, the cat sees mice and birds, and obstacles like trees and rocks, as identifiable modules. Cluster analysis can be used (explicitly or implicitly) to recognise that each of the components of the chair are highly interelated with each other, but largely isolated from the things around them (I can move all the components of the chair as a single unified whole, without needing to factor in the weight of the lampshades, and coffee cups that happen to be near by). This seems connected with Max Tegmark's symmetries within a type-IV class of multiverse: that they are determinable even from within the system.
A river, or a star like the sun, can be a turbulent chaos within, but a snooker-ball-like, black-box, timeless simplicity outside. The amount of externally visible motion would have been dwarfed by the amount of internal motion, had it not been for the way that all that internal motion can be cancelled out and ignored from our calculation. The ratio of the two amounts could be considered to be some sort of Strouhal-like ratio: outwardly visible energy trend versus the amount of energy that is flapping around inside. For simple harmonic motion, the ratio of energy in one store versus that in the other follows a sin(ωt+0)/sin(ωt+π/2) curve, namely tan(ωt). This merely tells us that the energy is periodically swinging from one store to the other. One of Carnot's great insights was that, by noting the parameters at successive returns to the same state round the cycle, all the periodic fluctuation of the energy distribution can be left out of the calculation, in a way somewhat akin to taking a carefully chosen moving average, allowing the designer to focus just on the underlying trend in the flow of energy to heat and work.
Creation of semantics, and the meaning of "meaning"
Each cycle of the locomotive on the Turing track, laying down a story (beginning-middle-end) that is cyclic and well-rounded in itself. This section has addressed: top-down versus bottom-up working and dialogue and brainstorming and ontological versus epistemic.
Each time round the outer loop, inverting an axiom chosen at random (like mutation) or putting it in a different context (like crossing-over) or relaxing a constraint, or simply applying a perturbation to the status quo (like introducing tension in a piece of music, or setting the plot in a story). This leads to punctuated evolution.
The measurement problem can be equated to the establishment of meaning. In It from Bit, Wheeler cites D.Føllesdal (1975) ("Meaning and experience' in "Mind and language" (S.Guttenplan, ed.) Clarendon, Oxford, pp25-44). He seems to assume that 'meaning' (and hence 'semantics') are to be implemented via the communication of information in large quantities, not unlike the way that Hofstadter assumes that consciousness is achieved by passing a certain threshold of complexity.
Concluding remarks
This section has considered Top-down versus bottom-up working and Dialogue and brainstorming and Ontological versus epistemic and Black-box modular identity and Creation of semantics, and the meaning of "meaning".
Comparative control experiments, and a generalised parallax effect. Kirchhoff's voltage (symmetry) and current (conservation) laws: latency and throughput of pipelines, and the devices of Shannon, Carnot and Turing. Probabilities expressed as half-life. The selective (symmetry-breaking) properties of resonnance, filters, and generalised standing-waves.
Emergent behaviour supported on a sea of lower-level cycling and turmoil
A simple late-1970s computer game with a crude representation of a cannon near the left bottom corner of the video screen, and an enemy boat near the right bottom corner. The trajectory of the cannon ball was calculated incrementally, with the following three lines at the centre of the innermost loop:
x := x + dx; y := y + dy; dy := dy - g; (where g represents the acceleration due to gravity)Running the programÉ the cannon ball traced a beautiful parabolic path from the cannon towards the boat. But where did that parabola come from? It was not typed in explicitly, but emerged, implicitly, from the above three lines of code. This would be an example of emergent behaviour that is based on a deeper knowledge of the lower levels, and an element of surprise at how they come together.
In the chapter after next, the implications of a series of inner cycles within an overarching outer cycle, nested recursively to many layers, is considered. This chapter started by considering how each machine class might be built on parts of the previous machine class. A thought-experiment was introduced to implement a universal Turing machine as a steam locomotive read/write head running forward, then back, on a Turing tape railway track. By analogy, the aim would be that meaning might be created by running computer execution backwards and forwards repeatedly; we could set about stopping a computing machine from making the usual progress through program execution, to implement the next MC. BubbleSort was considered, in which the backward execution does not restore the original jumbled sequence, but just a similarly jumbled sequence. The training data, or fitness function, is applying the top-down influence on the execution, while the annealing is providing the bottom-up manipulations. In the case of natural evolutionary systems, though, there is no top-down mechanism, and it is serendipity and persistence (regions of convergence within the peaks and troughs of the landscape) that are the nearest to top-down influence. (Empedocles noted that stable structures persist while unstable one tend to fade away, by definition,. Meanwhile, material can fall into an astronomical gravity well, at exponentially increasing rates, without cease, just until the point that symmetry is broken by some non-linearity, and the sub-stomic degeneracy pressure, of one type or another, starts to push back against it.) Lastly, this feeds back into the thesis of the self-writing story, and how the paragraphs are being shuffled back and forth by cut-and-paste, and are gradually converging on telling their emergent story.
Since computer evolutionary systems feature so heavily in this chapter, the next chapter takes a step aside to consider a few potential definitions of terms that have defied being so defined over the past centuries. Alternatively, the reader is referred back to the table of contents.
map