Summary of Electromagnetism Definitions

For historical reasons, the first part of the story involves imagining two extremely long lengths of bare electric wire, laid out parallel to each other, exactly one metre apart in free space, in two perfectly straight lines. An electric current is made to flow down one wire, and then back along the other, and the extremely weak repulsion between the two wires is measured. The electric current in the two wires is adjusted until the force is exactly 2x10^-7N for each metre section of the pair of wires. The electric current when this happens is exactly 1 A.

This might sound a bit contrived and arbitrary, but one way or another, a human-inspired definition had to be made somewhere, and this happens to be the one that physicists have found convenient. The factor of 2 was chosen partly because there are two wires contributing to the force, but more because it puts intuitively reasonable constants into later equations (such as those that describe fields round spherical and cylindrical charge carriers). The factor of 10^-7 was chosen to make the unit useful for practical purposes. Even today, the definition of the ampere remains a good compromise for both electronic engineers, who routinely work a few orders of magnitude below this value, and electrical engineers, who routinely work a few orders of magnitude above it. In fact, the factor of 10^-7 originates from our definitions for the units of length and time, and hence from the value for the speed of light. Taking the discrepency of the factor of 30 into account (the speed of light being about 3x10⁸ m/s, rather than 10⁷) electronic engineers routinely work with resistors that are a few orders of magnitude bigger than 376 ohms (=30x4π), and electrical engineers routinely work with resistances that are a few orders of magnitude smaller.

Electricity

Electric charge

If one amp of electric current (I) flows along a wire for one second (into a capacitor, for example), then, by definition, the amount of electric charge (Q) that has arrived is one coulomb (Q=I.t).

Force (electrostatic)

Now, suppose we place two electric charges, Q₁ and Q₂, (each one stored on a spherical capacitor) a certain distance apart, r. Experiments show that the repulsive force between them is proportional to Q₁.Q₂/r².

Suppose that there is a small object placed somewhere out in empty space, charged up with an electrical charge of Q₁. Without needing to touch the object, we can feel the effects of Q₁ on a suitable test probe, that we have charged up to Q₂, and can conclude what the magnitude of the distant charge is. We can set Q₂ to any value we like, as long as we scale appropriately afterwards, so it is convenient to hold it constant at unity (one coulomb, 1 C).

To help analyse this further, it is convenient to define four slightly abstract properties: the electric flux (ψ), the electric flux density (D), the electric field (E), and a last one that I will call the total electric field.

Total electric field

We can think of lines of electrostatic force emanating from the distant object, and we just need to go all the way round the object, like some sort of miniature Starship Enterprise, always at some (arbitrary, and not necessarily constant) distance from it, counting up the total number of these lines of force. Of course, the summation needs to be done in three-dimensional space. We could do the summation over a spherical shell surrounding the object, though in fact the summation would give the same value regardless of the shape of the shell that we traced out.

Having counted up the total number of lines of force, we would have a value for the total electric field that surrounds the object. This is proportional to the electric charge, Q₁, on that object, with the constant of proportionality defined as 1/ε.

This, in effect, is the basis of Gauss' Law for electric fields.

Electric field

Thus, the total electric field is Q₁/ε, and radiates out in all directions. At any distance, r, from the object, the total electric field over the whole spherical measurement area is still the same, but spread out more and more thinly with increasing distance from the object, r, in proportion to the increasing surface area of the sphere. Thus, if our test probe has unit cross-sectional area, it would find that the electric field had a value of Q₁/(4π.ε.r²). And, taking the charge on the test probe, Q₂, back into consideration, again, this means that repulsive force between two charged bodies is Q₁.Q₂/(4π.ε.r²), and hence that the electric field is the force on unit charge (E=F/Q₂).

Electric potential difference and electro-motive force

Next, since Watts=Volts.Amps, it follows that Volts=Joules/Coulombs, and hence that any potential difference=work/charge. To make the Watts=Volts.Amps relationship come out, the volt is defined as the potential difference created when unit work is done by a unit charge.

When the physical system is driven in the other direction, unit work is done by a unit charge when it is driven by an electro-motive force of 1 volt.

Electric capacitors

Parallel-plate electric capacitors

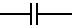
A capacitor can be made from two parallel metal plates, each of area A, that are separated from each other by a thin layer of insulator, of thickness d. Thinking of one plate as the ground plate, and taking one unit of charge (1 coulomb) from it, and putting it on the other plate, involves doing work, and causes a voltage difference to be created between the two plates. The voltage is proportional to the amount of charge transferred, with the reciprocal of the constant of proportionality being defined as the capacitance of the capacitor (V=Q/C), measured in Farads.

The total electric field is still Q/ε and so the electric field is Q/(ε.A). Since the electric field is the force on unit charge, the electric field times distance gives the work per unit charge, which is the definition of voltage. Thus V=Q.d/(ε.A), and so C=ε.A/d.

Spherical electric capacitors

For a spherical capacitor, of radius a, of the type used in electrostatics apparatus, it is convenient to view the electric field first from a distance, x. The electric field (E) is Q/(4π.ε.x²). With the parallel plate capacitor, the field is uniform, and all the lines of force are parallel. With a spherical capacitor the lines of force radiate out, and become more widely distributed with distance. For the parallel plate capacitor, a simple linear multiplication of the field by distance was valid (since ∫dx, from x=0 to x=d, is d); for the spherical capacitor, the multiplication is by incremental distance, dx, and the integration needs to be performed to get the result for the total distance. Thus, the work done (W) in transferring unit charge from ground to the spherical capacitor involves a voltage that is Q/(4π.ε).∫(dx/x²). The charge is taken from an infinite distance away, and is placed on the surface of the sphere, at distance (a) from the centre (since all of the charge distributes itself around the surface of the object). Thus, the integration is performed between infinity and a, giving V=Q/(4π.ε.a) and hence the capacitance, C, is 4π.ε.a.

Electric dipoles and electric monopoles

An electric capacitor, and most graphically a parallel-plate capacitor, acts as an electric dipole: one part of the device is as negatively charged as the other part is positively charged. Lines of electic field eminate from the positive part, and loop back to the negative part in exactly equal numbers; overall, therefore, the device is completely self-contained, and electrically neutral (which is why electrical capacitors do not attract any more dust than their neighbouring electronic components.

Notably, molecules can act as electric dipoles, with one part of the molecule being negatively charged, and another part equally positively charged. This results when exta electrons are attracted by one atom in the molecule, away from one of the other atoms.

The electron is an electric monopole. It carries an overall negative charge, and is (by definition) not electrically neutral. Lines of electric field radiate into it.

Electric flux and electric flux density

The electric flux (ψ) and electric flux density (D) have not been used in this analysis, but are related to the total electric field, and the electric field (E), respectively, by a simple factor of ε. This means that the electric flux (ψ) is numerically equal to the total amount of electric charge (Q) that is contained anywhere within that volume. There is a difference, though. The charge is the amount of electric charge physically on an object, whereas the electric flux is a measure of that charge felt by the test probe working at a distance, perhaps quite a large distance, without needing to know anything about the object itself. Similarly, the electric flux density (D) is related to the charge density (that is the amount of electric charge per unit area).

Magnetism

The exactly corresponding chain of definitions can similarly be applied to magnetism, in particular, we are interested in the four parameters for: the magnetic flux (φ), the magnetic flux density (B), the magnetic field (H), and a last one that I will call the total magnetic field.

Magnetic monopoles

Magnetic dipoles

Even though no experiment has yet observed a magnetic monopole particle, and it is fairly safe to assume that either they do not exist, or that they exist only in very restricted contexts that evidently do not affect the operation of mobile telephones on earth), we can still make use of the symmetry.

The role of magnetic charge is, instead, played by incremental lengths of flowing electric currents (μ.I.dx) that generate magnetic dipoles (with both north and south poles, one present at each end).

Magnetic field, magnetic flux, and magnetic flux density

Thus the total magnetic field is I.dx; the magnetic field, H, is I.dx/(4π.r²); the magnetic flux, φ, is μ.I.dx; and the magnetic flux density, B, is μ.I.dx/(4π.r²).

It should be noted, here, that not everyone adopts the same terminology for these parameters, and that the world of magnetic fields has not standardised its terminology to the same extent that the world of electric fields has. In particular, what is referred to, here, on this page, as the "magnetic flux density" (B), is variously referred to, in other texts, as the "magnetic induction", or the "magnetic field in Teslas" (as opposed to the "magnetic field in Webers", H). Also, there is one small fly in the neat story, above, and that is that the influence of the intervening medium, expressed by 1/ε, appears in the equations for the electric field parameters and is absent for the electric flux parameters, while μ appears in the equations for the magnetic flux parameters and is absent for the magnetic field parameters.

Force (magnetic)

Just as an electric field is defined it terms of a force applied by the distant source on a standard test probe (1 coulomb), so the magnetic flux density generated in the vicinity of one current-carrying wire: B=μ.I.dx/(4π.r²). For two extremely long, parallel electric wires, as used in the definition of the Ampere at the top of this page, the dx term involves integrating a sin(θ) term, for the angle subtended at the test point by each of the sections of the other wire. At the end of the integration, it turns out that the force exerted on a test probe wire, of length L, is B.I.L. Since this force was defined as 2x10^-7N when the current in the other, infinitely long, wire is unity (1 A), it follows that B, in this case, is 2x10^-7T, and that μ has a value of 4π.10^-7 for free space. Thus, μ, is not a universal constant (a property of the universe) at all, but is fixed by our particular choice of definition for the ampere. Likewise, ε is not a constant of the universe, either, but has a value that is fixed as soon as we have defined μ. In fact, the relationship is c=1/√(μ.ε); so, once μ is fixed by definition, ε also has its value set, based on the velocity of light.

Magnetic flux density

If we now wind a coil, in the form of a hollow cylinder with a radius, a, we can calculate the magnetic flux density, B, that runs down the central axis of the coil. The multiple turns of the coil behave as wires layed side by side, each carrying the same current, and each one 2π.a in length. This turns out to give B=μ.N.I.[cos(θ1)-cos(θ2)]/2, where N is the number of turns per unit length along the side of the cylindrical coil, and θ1 and θ2 are the angles subtended from the chosen point along the central axis by the two ends of the coil. For a short coil (a ring of coiled wire taking up negligible length) this tends to B=μ.n.I/(2.a), where n is the total number of turns in the coil. For a long coil, the original expression tends to B=μ.N.I deep in the heart of the coil, tailing off to B=μ.N.I/2 at each end.

Magnetic inductor

The magnetic flux (the total flux density) in the long coil is φ=μ.N.I.A (measured in webers). When the current is made to vary, the rate of change of flux, dφ/dt is μ.N.A.dI/dt. This induces a back EMF (a voltage) as it cuts through each turn of the coil. Since N is the number of turns per unit length along the side the cylindrical coil, there are N.h turns, where h is the length of the cylindrical coil. Thus V=μ.N².h.A.dI/dt. But the definition of inductance, L, is V=L.dI/dt, so the inductance of the coil, L, is μ.N².A.h (or, perhaps more usefully, μ.n².A/h).

Units and Values

All of the above discussion stems from a single definition – that of the ampere as the unit of electric current (I). From this, the units of each of the other invented quantities can be derived. Electric charge (Q) is measured in ampere-seconds, which is abbreviated to the coulomb. Electric flux (ψ) is also measured in units of coulombs, so electric flux density (D) is measured in units of coulombs per square metre. The electric field (E) could be measured in units of newtons per coulomb, but is more usually measured in volts per metre (the two are completely equivalent). Lastly, electrical capacitance (C) is a measure of coulombs per volt, which is abbreviated to farads.

Returning to magnetic fields, this means that magnetic charge (Q), and hence also that of magnetic flux (φ), are measured in units of newtons per ampere-metre, or henry-amperes, both of which are abbreviated to webers. The magnetic flux density, B, is therefore measured in webers per square metre, which is abbreviated to teslas. The unit of MMF, V, turns out to be the same as that of electric current, namely the ampere. Consequently, magnetic fields, H, are measured in amperes per metre.

The exotic magnetic device, with two parallel plates separated by an insulating material with a high magnetic permeability (such as iron) turns out to be an inductor, with a magnetic capacity measured in henries. In reality, of course, we make inductors from coils of wire carrying electric currents, rather than parallel plate devices storing hypothetical magnetic monopoles.

Electric circuits and magnetic circuits

Permativity and permiability

The two parameters, ε and μ, were introduced, earlier, as being constants of proportionality. However, they are not necessarily constant under all conditions. They are normally each split into two parts: ε=ε₀.ε_r and μ=μ₀.μ_r. The part with the zero as a suffix is the value for free space, and is a proper constant; the part with an r as the suffix is the relative value of the actual material, and is a dimensionless scalar. μ₀ is defined as 4π.10^-7 H/m, as already noted. Since the speed of light, c₀ is now defined (since 1983) as 299792458 m/s, the value of ε₀, measured in F/m, is also fixed, 1/(c₀.√μ₀).

Typical values for ε_r over the expected range of electric fields are: 2 for perspex, 5 for mica, 8 for oil, 80 for water, 2000 for tourmaline. Typical values for μ_r over the expected range of magnetic fields can be around: 2000 for nickel, 7000 for iron. Although ε_r and μ_r are dimensionless quantities that scale for substances other than free space, they are not necessarily constants.

Permanent magnets

μ_r is most markedly not a constant (except for a vacuum, where μ_r=1 is indeed a constant). Its value tails off to very small values for large magnetic fields. Thus, plotting the curve for B=μ₀.μ_r.H does not produce a straight line passing through the origin, but an S-shaped curve that saturates at maximum flux density, B_sat, for large magnetic fields. Moreover, the curve does not pass through the origin, but passes just below the origin as H is increased through zero from negative to positive values, and passes just above it as H is decreased through zero from positive to negative values. That is, the alternating magnetic flux density lags behind the magnetic field that is causing it. The amount by which it passes above or below the origin is called the magnetic remanence, B_r, and is a measure of how good the material is at acting as a permanent magnet, in the absence of any energising magnetic field.

Another way of phrasing the same phenomenon is that the curve passes just to the right of the origin as B is being increased through zero from negative to positive values, and just to the left of it in the other half of the cycle. The amount by which it passes to the left or right is called the magnetic coercitivity, H_c, and is a measure of how strong a magnetic field would need to be applied to a permanent magnet in order to de-magnetise it.

Fleming's rules for motors and generators

A simple illustration can be given as to why we need to have two rules:

• Fleming's Left Hand Rule for electric motors
• Fleming's Right Hand Rule for electric generators

If we consider an electric, battery-powered vehicle that uses its motor for regenerative braking, as soon as the fully charged battery is switched out, and the fully discharged battery is switched in, current flows in the opposite direction in the connections to the motor/generator; and yet, the direction of the vehicle, and hence of the motor parts, and the direction of the magnetic fields of the permanent magnets inside the motor generator, each remain unchanged. As to how the vehicle knows whether to charge or discharge the battery, this follows from the second law of thermodynamics, where energy flow from the high-energy source to the low-energy source (fully charged battery to the wheels, or wheels to the fully discharged battery).

It is also worth noting that, in mathematics, the vector cross product is defined as a rule that is remembered using the right hand. This means that the force on a electric-current carrying conductor in a magnetic field, (F=B.I.L when expressed as a scalar value) is expressed as a vector quantity as F=(I.L)xB, with the allocation to the fingers reversed compared to those of Fleming's rules, to compensate (by double negation) for the change of hand.

Maxwell's equations

These can be summarised as follows:

Gauss' law for electric fields

∇ . D = ρ

Ampere-Maxwell's Law

∇ x H = J + ∂D/∂t

Gauss' law for magnetic fields

∇ . B = 0

Faraday's Law

- ∇ x E = 0 + ∂B/∂t

The integral form of Gauss' law for electric fields was sketched out, in words, when describing the total electric field round a body that carries an electric charge. Using the divergence theorem, it converts to the differential form shown above, where ρ is the electric charge density (in C/m³).

The first equation is, in effect, a generalisation (in smooth and continuous 3D space) of Kirchhoff's current law, for electric monopoles (such as electrons). The second equation calculates Oested's magnetic field, noting that it occurs around current-carrying wires, plus around dielectrics with a varying electric field. The third and fourth equations then do the same for magnetic monopoles, but note that the number of magnetic monopoles in our universe is zero).

Ampere-Maxwell's law is, in effect, an expression of the Corkscrew Rule (also known as Ampere's Right Hand Rule). It follows, then, that, Faraday's law is, in effect, an expression of Faraday's Left Hand Rule. Rather than invent a new symbol to represent the left hand vector product, it is simply necesary to put a minus sign, on the left hand side of the equation, to invert the normal vector cross product. This explains what the minus sign is for, but does not explain why one rule has it and the other does not; but, one rule talks about voltages (and electrostatics) in terms of currents (and magnetics), while the other talks of currents in terms of voltages. If V(t) is sinusoidal, which Fourier's analysis tells us it inevitably must be, then I(t) is cosinusoidal (because you either differentiate it, or integrate it, in Maxwell's equations), then, the other rule brings us back to V(t) again by differentiating (or integrating) again, to make it negative sinusoidal. It is inevitable that Faraday's and Ampere-Maxwell's rules must have opposite signs (and for current to lead or lag voltage by π/2 because of the relationship between sin and cos).

Div, Grad and Curl

There qre already plenty of very good introductions to Div, Grad and Curl in text books and on the internet. This section is aimed just at giving a intuitive, sketch-like view of what they are.

To stqrt off, imagine using a computer program to simulate a large volume of gas in an enormous container (air in an empty oil tanker out at sea, for example) with an extremely sudden high pressure source near its centre (such as the detonation of a small explosive held dangling near the centre). The computer program logs the pressure at each point throughout that volume (every little cube-like voxel, one centimetre on a side, in a 3D grid throughout the container).

To simplify even further, for the moment, just imagine a 2D slice through this volume, plotted out on paper as a map of pressures, not unlike a geographic map of heights above sea-level. Instead of contours (as on the geographic map) these would be marked with isobars (as on a weather map) tracing out the positions of the little cubes that are at the same pressure as each other. If the detonating explosive did not detonate evenly, there would be a central peak, with ridges protruding in several directions. The computer program could maintain a second copy of the matrix, but with pressure slope information at each pixel, instead of an absolute pressure value. This matrix would be the same as having applied the GRAD operation to the original data. It gives a summary of the pressure gradient at each pixel.

Setting up another matrix on the computer, one could log the total immigration of particles (molecules) from each voxel/pixel (that going out across the North side, minus that across the South side, added to the difference of that across the West side, minus that across the East side). This matrix is equivalent to having performed a DIV operation on the original matrix of currents, and gives a summary of the amount of divergence of the particles (from the central point where the small explosive was detonated, for example).

The above example is for a compressible fluid, like air. If it is non-compressible, like that of electromagnetic fields, the result is always zero for all voxels that do not contain a source (an electric monopole like an electron, instead of the explosive device in the example given above). In this context, the divergence operator becomes a sort of generalisation of Kirchhoff's current law (the sum of all the currents flowing into a given point is zero).

For the CURL operation, a different analogy is needed: that of roughly-torn clumps of grass one-third of the way across the river as it passes under a bridge. Rushing over to the other side of the bridge, the circular floating island of grass emerges, but gently turning as it flows down the river. The answer the question as to how fast it is turning is obtained by performing a CURL operation on the matrix for the water flow in each pixel of the river. Because the pixels closer to the centre of the river, either side of the position one third of the way across the river, is flowing slightly faster than that in the pixels closer to the river bank. So, there is a net torque on the island of grass. (The convention is to specify the CURL as a vector whose direction is in the direction of the axis of the spin; if the clump of grass is rotating anticlockwise, like the curled up fingers of a clenched right hand, the vector's direction is vertically upward, like the thumb of that right hand.)

The next step is to imagine generalising all of this from 2D to 3D (from pixels to voxels). It is no coincidence that the notions of DIV and CURL fit so well into Maxwell's equations. Maxwell invented them precisely as tools for expressing his equations.

Conclusion

Each of the paragraphs on this page that brought in new terms, did so by way of definition – except for just one paragraph (the one equating μ.N.A.dI/dt to volts). When the volt was first mentioned, in the context of work (measured in J) being done on moving a charge (measured in C) in an electric field, it was by way of definition of the volt. Now, though, the volt has turned out to be the EMF induced in each turn of a coil when the magnetic flux cutting through it varies at a particular rate (measured in Wb/s). This is no coincidence, of course. It is just a result of magnetism and electrostatics not being distinct forces at all, but two aspects of a single fundamental force.

Interestingly, this example illustrates well how context changes the way that we view any given fundamental force. In the case of the electromagnetic force, the scale of the machine is what tends to distinguish electric from magnetic: our large electrical machines see the force predominantly as a magnetic one (we do not build large electric motors that use electrostatic attraction to give them their turning moment), while our small electrical machines see it predominantly as an electrostatic one (we do not build magnetic-field effect transistors). That is not to say that the other aspect is absent, just that it is not predominant (constructors of large magnets still have to worry about the problems of arcing, and those of integrated circuits the problems of transmission line inductance).

This was considered worth mentioning because, by extension, it suggests why the weak nuclear force, and strong nuclear force, appear to us to be so different, at the very least in strength, in comparison to the electromagnetic force. If, indeed, the three can be unified, and viewed as manifestations of the same fundamental force, our perceived distinction between them is merely caused by the change of context in which we tend to view each of them.